Library
|
|
| Print Free Pamphlet - -
Brief Summary Sections :
Introduction
|
|
|
The Number 153 Was Very Prominent and Recognizable in Ancient Greek Culture In modern speech a person can use the number 3.14
and or the number 9-11 to convey a meaning that is much greater than
just the numerical value. And he knows that the average person will
associate the appropriate meanings that go with those numbers. And he
can be reasonably assured that the person will make the proper
association without him having to explain it. Today we usually express the values of irrational numbers as below. π = 3.14… e = 2.71828… Now, π does not equal 3.14. The dots following the numbers above denote that this is just an approximation. The value of Irrational numbers when expressed using digits can only be expressed by way of approximation when using digits. In an exact equal equation the numbers would go on forever and therefore, be impossible to write. See endnote on Irrational Numbers. See separate article on how Greek Culture : √3 and 153 As demonstrated below the √3 figured very prominently in ancient Greek culture. It is also an irrational number. So, its value when expressed in digits can only be done by way of an approximation. The closest approximation of √3 when using small whole numbers is
And since they did not have the decimal system they did use this approximation as the best possible. It is the most accurate while still being manageable. This is because mathematical computations become very elaborate when using large denominators. And finding the lowest common denominator is essential to combining fractions. However, at the time John had written his Gospel since the Greeks also did not yet have the horizontal fraction bar so, they would have written it as √3 ≈ 265 : 153. So, 153 is essential as the final number when expressing the value of √3.
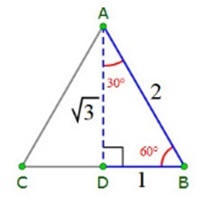
And the value of √3 figures quite prominently in geometry which was the core of the Greek cultural view of the world and those things important to them. Notice below how prominent the equilateral triangle is in Greek culture. See below. . The height of an
equilateral triangle with a measure of two is √3. 30° -
60° - 90° Δ Triangles. |
|
|
|
|
|
Conclusion
“Let no one ignorant of geometry enter here.” All the elements of creation could, in their view, be reduced to the geometric shapes of the solids of Plato and Archimedes. |
|
| The √3 had to be expressed, as close as reasonably possible, in
rational terms in order to calculate distances for example. So, the
final number in value for √3 was the number 153. √3 ≈ 265 : 153 Greek philosophy and mathematics was highly valued in ancient Greek culture. So, John knew he could safely use 153 as an allusion. It would bring to mind in his Greek parishioners the great Greek mathematician Archimedes and their philosophers who made extensive use of that number. That number would bring to their minds Greek wisdom just as surely as 9-11 brings to our minds the events in New York City on September 11, 2001. |
|
| End note An irrational number is a real number that cannot be expressed as a ratio of integers, i.e. as a fraction. Therefore, irrational numbers, when written as decimal numbers, do not terminate, nor do they repeat. For example, the number π and √3 are irrational numbers. The number π the starts with 3.141592653589793238462643 … but it goes on forever and ever. |
|
| Continue ... Sections :
Introduction |
|
|
|
|
||||
|
||||
|
||||
|
||||
|
||||