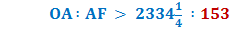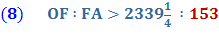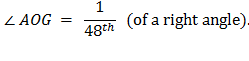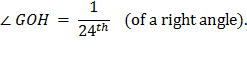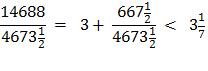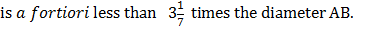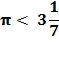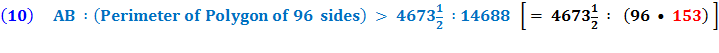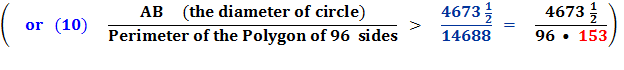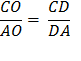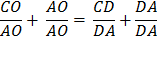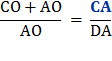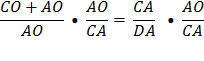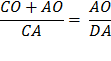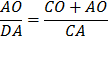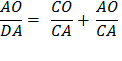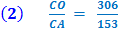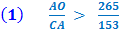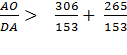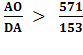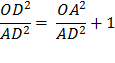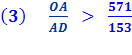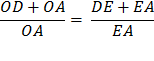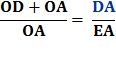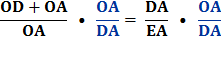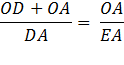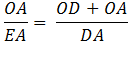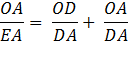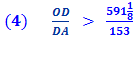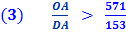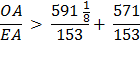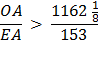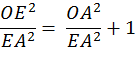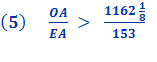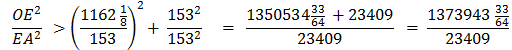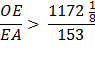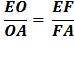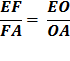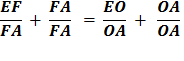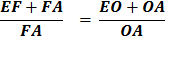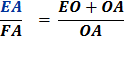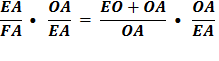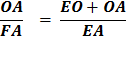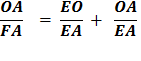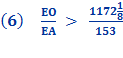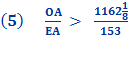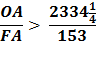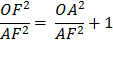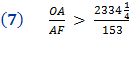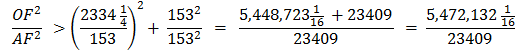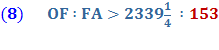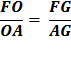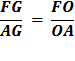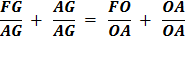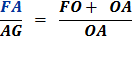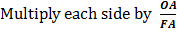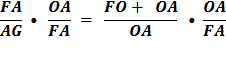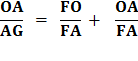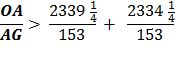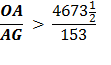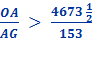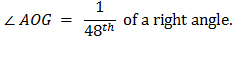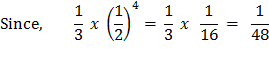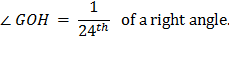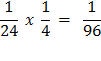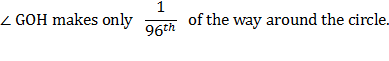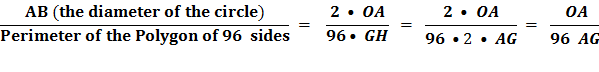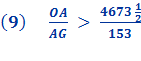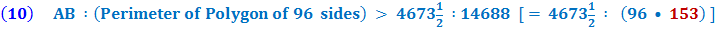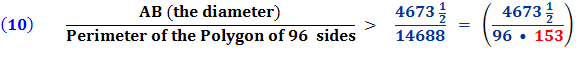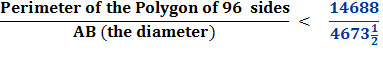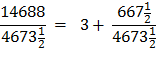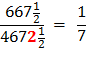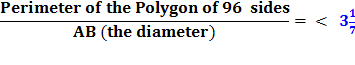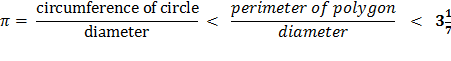Library
Read 153 Fish
|
|
|
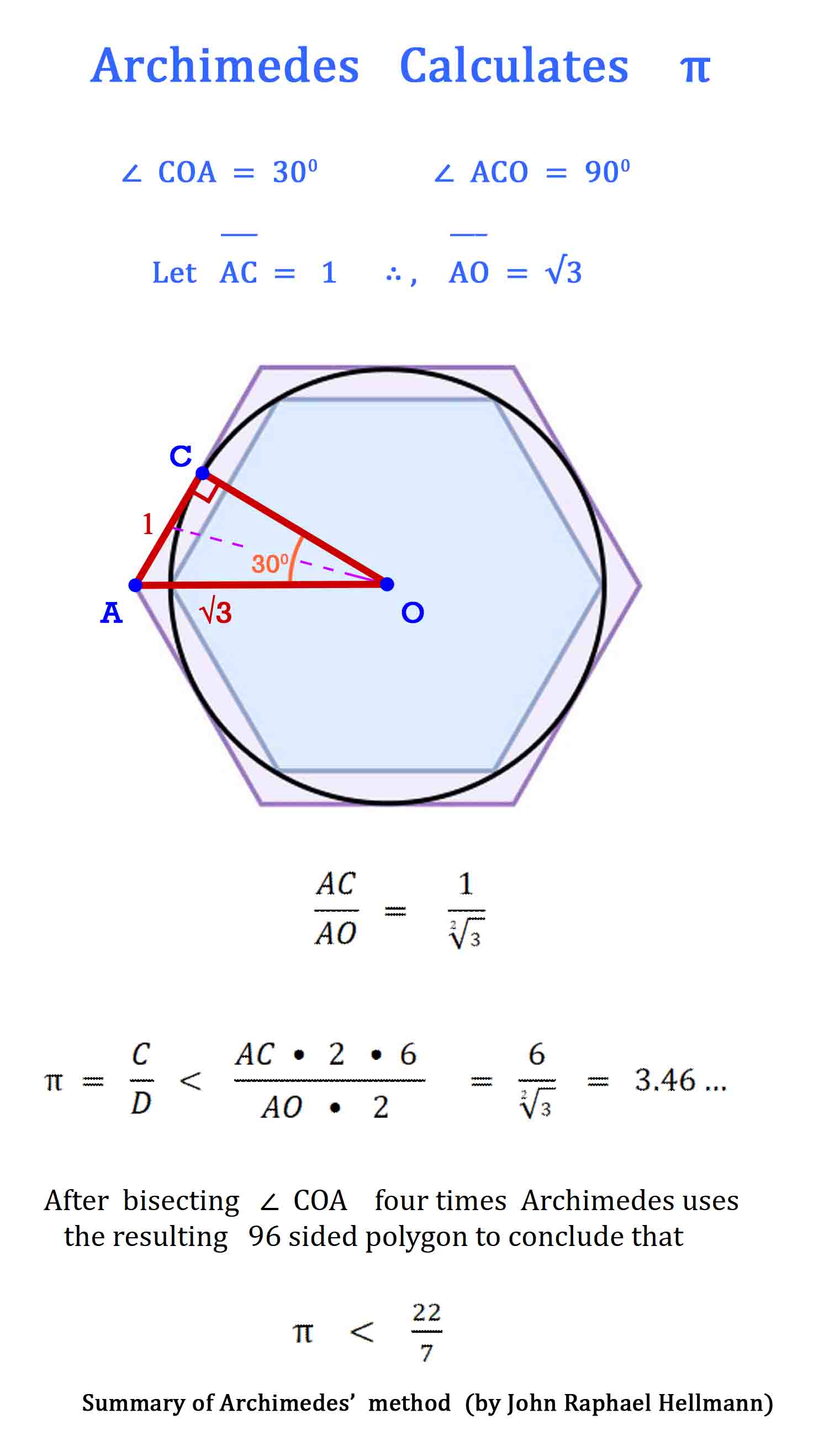
Archimedes Calculates Pi
In
Archimedes’ first section, he calculates Pi, π, to be slightly less than
3 and one seventh. Summary of Archimedes’ method
|
|
|
|
|
|
Archimedes does not work out all the math on paper (actually parchment or sheepskin.) Most of the portions in brackets [ ] were added by Heath in 19th century. Notice how the equations end with 153. |
|
| See below, Archimedes Math Made Simple and Easy For a detailed explanation of all the mathematical steps that prove the 10 conclusions below, click on the number for that equation. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, Conclusion
|
|
| Words below in brackets [ ] and parathesis ( ) are added for clarity. | |
| Archimedes’ actual text
[translated into English ] begins :
|
|
|
|
|
|
|
|
|
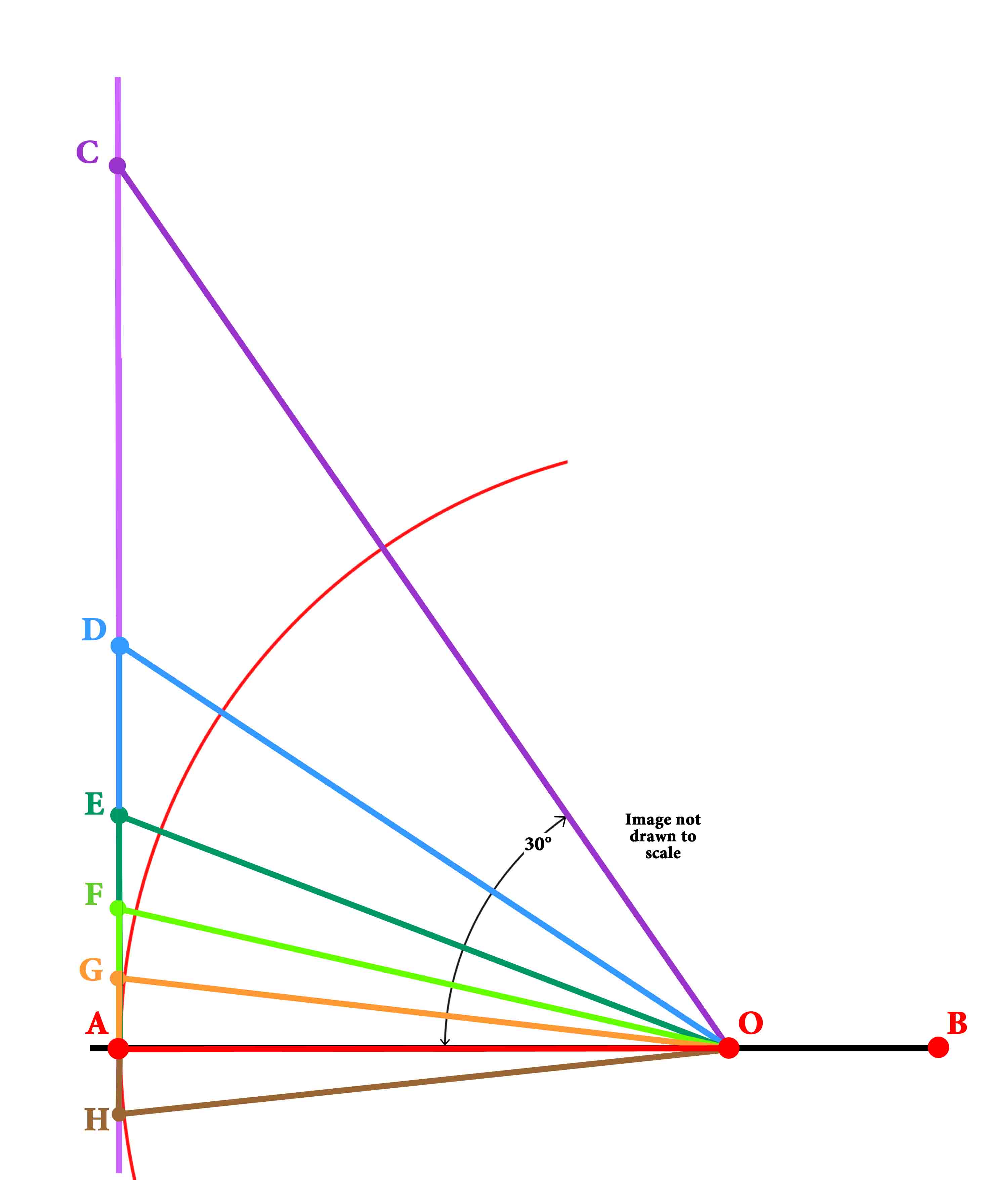
I. Let AB be the diameter of any circle, O its center, AC the
tangent at A; and let the angle
∠ AOC be
one-third of a right angle. Then
And
First,
draw OD
bisecting the angle
∠ AOC and
meeting AC in D. so that Therefore
Hence
so that Secondly, let OE bisect
the angle ∠
AOD, meeting AD in E.
Thus Thirdly, let OF
bisect the angle
∠ AOE and meet AE in F.
Thus
Fourthly, let OG bisect
the angle AOF, meeting AF in G.
Now the angle ∠ AOC, which is one-third of a right angle, has been bisected four times, and it follows that angle
Make the angle ∠
AOH on the other side of OA equal to the angle
∠ AOG, and
Thus GH
is one side of a regular polygon of 96 sides circumscribed to
the given circle.
while it follows that
But
Therefore the circumference of the circle (being less than the perimeter of the polygon)
End Quote: So, Conclusion :
|
|
|
And notice above that almost all the equations end with the number “153.”
So, in equation 10 Archimedes multiplies his denominator 153 times 96 to get 14688. Is this by pure chance that these equations end with 153 ? Rather, it is an indication of the brilliance and the simplicity of the design of Archimedes’ solution for solving for Pi, π. Archimedes had brilliantly laid a 30° - 60° - 90° Δ Triangle with the longer leg along the diameter and the other leg of the triangle as a side of a polygon going closely around the circumference of the circle. This set up a ratio of
By using this denominator of 153 in each equation he was able to calculate π. |
|
|
For a detailed explanation of all the mathematical steps that prove
Archimedes 10 conclusions above, click on
the number for that equation to see Archimedes Math Made Simple. |
|
|
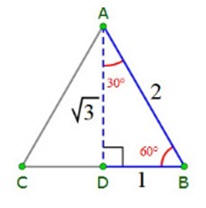
Archimedes Math Made Simple This section below details all the mathematical steps that lead to the ten conclusions Archimedes makes above in calculating Pi, π. Previously when mathematicians wanted to calculate the value of Pi, π, they measured the circumference of a circle and divided it by the measurement of its diameter. However measurements are inherently inaccurate when a person is trying to arrive at three or more significant digits. In an ingenious way Archimedes developed a new method that did not involve measurements at all. It is based on pure mathematical calculations. His method allowed a person to calculate the value of Pi as accurately as one desired. Because the method was pure mathematics the answers were indisputable. A 30° - 60° - 90° triangle has unique characteristics such that the ratio of the longer leg to the shorter leg is √3 :1. By constructing such a triangle such that the longer leg is along the radius (or diameter) of any give circle and the shorter leg is along a tangent outside of the circle Archimedes sets up this ratio of √3:1 for his method of determining the value of Pi, π. This outside tangent is used to calculate the measure of a polygon constructed just outside of the circumference of the circle. Constructing the triangle in this way places the value of 1 in the denominator which makes his calculations much easier.
|
|
|
|
|
|
|
|
|
|
Proof for (1)
Properties of
a 30° - 60° - 90° Δ Triangle
In order to make the mathematical computations, Archimedes needed to substitute a rational number for √3, so he used this very close approximation for √3.
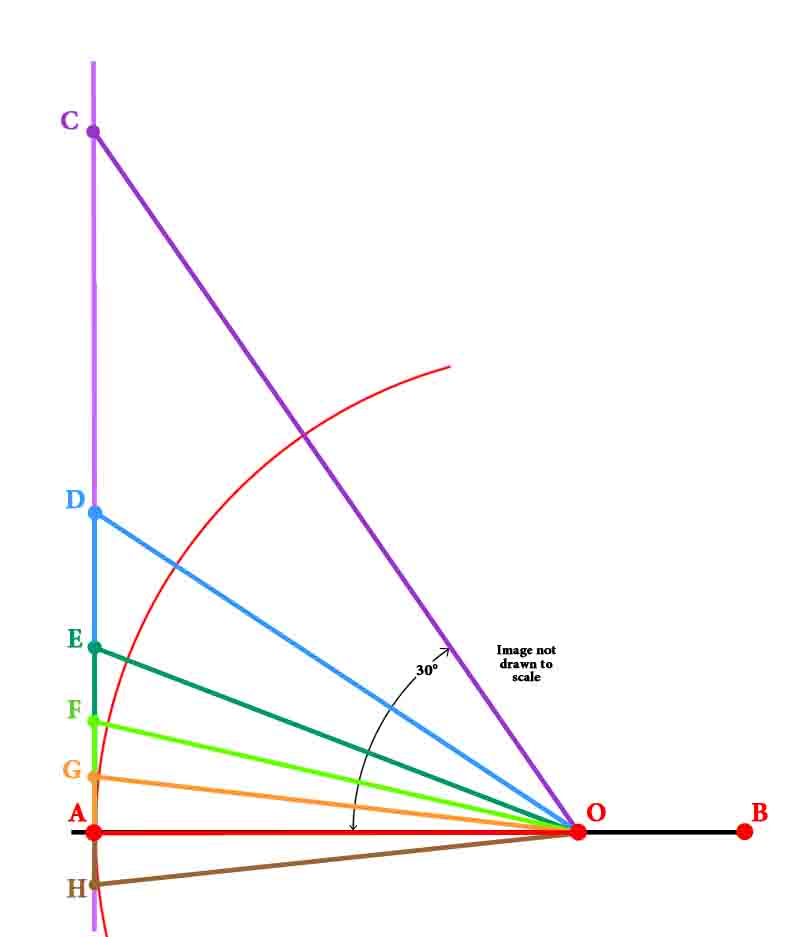
I. Let AB be the diameter of any circle, O its center, AC the tangent at A; and let the angle ∠ AOC be one-third of a right angle. (See diagram on right.) Then (1) AO : CA =[ √3 : 1 ]
Conclusion 2, below, as also in conclusion 1, is deduced from the Properties of a 30° - 60° - 90° Triangle. See above. and (2) CO : CA = [ 2:1 ] . First, draw OD bisecting
the angle ∠ AOC and
meeting AC in D. See : Euclid’s Elements : Triangles Book 6, Proposition 3
Add 1 to each side.
Since the measure of lines CD + DA = CA
Multiply each side by
Reverse equation.
Substitute using statements 2 and 1 above. |
|
Therefore, Therefore
Using the Pythagorean Theorem, OD2 = OA2 + AD2 Divide each side by AD2
Substituting using line (3.)
Hence
The next step is to simplify and take the square root of each side. Again, in order to make mathematical computations Archimedes needs to substitute a rational approximation for the square root because it is an irrational number:
So,
so that
Secondly, let OE bisect
the angle ∠
AOD, meeting AD in E. Again using :Euclid’s Bk 6, Prop. 3, as when we made the first bisection of angle ∠ AOC So, OD : OA = DE : EA And again adding 1 to each side gives
Since DE + EA = DA
Multiply each side by
Reverse equation
Substituting using lines 4 and 3 Therefore,
As before, use the Pythagorean Theorem, OE2 = OA2 + EA2 Divide each side by EA2
Substituting using line
Taking the square root of each side,
This gives us line (6)
Thus Thirdly, let OF
bisect the angle
∠ AOE and meet AE in F. As in the previous bisections, we again use :Euclid’s Bk 6, Prop. 3, as when we made the first bisection of angle ∠ AOC
Reverse Equation
Add +1 to each side of the equation
Since EF + FA = EA
Multiply each side by
Substitute using lines (6) and (5). Therefore,
|
|
|
Proof for (8) Using the Pythagorean Theorem, OF2 = OA2 + AF2 Divide each side by AF2
Substitute using line (7) Therefore,
Taking the square root of each side,
So,
Fourthly, let OG bisect
the angle AOF, meeting AF in G. Again using :Euclid’s Bk 6, Prop. 3, as when we made the first bisection of angle ∠ AOC
|
|
Reverse equation
Add +1 to each side.
Since FG + AG = FA
Substitute using lines (8) and (7)
Therefore,
Now the angle ∠ AOC, which is one-third of a right angle, has been bisected four times, and it follows that angle
Make the angle ∠
AOH on the other side of OA equal to the angle
∠ AOG, and
let GA produced (extended to) meet OH in H.
Thus GH is one side of a regular polygon of 96 sides circumscribed to the given circle. Because,
And since, And since the diameter, AB is two time the radius, AO AB = 2 AO, And side GH = AG + AH. And, since AG and AH are mirror images, AG =
AH . GH = 2 AG, it follows that
Substituting line And since, 96 x 153 = 14688 we get
Proof for Conclusion: Inverting the ratio above give us
And since,
And since,
Therefore,
Therefore the circumference of the circle (being less than the perimeter of the polygon)
So,
In the next section, Archimedes goes onto inscribe a polygon within the circle and finds the lower limit of Pi. He concludes with the calculation that Pi is between the following limits. Final Conclusion:
|
|
| See the connection between Archimedes and the Gospel. Read 153 Fish |
|
|
|
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||